Module: Euler Number ()
For an introduction, see:
This module computes the Euler number which is an indicator of connectivity of an image.
The Euler number, or connectivity factor
, is related to the number of connected components
, and to the number of holes
in each of these components. The Euler number is defined as
.
For objects with no hole, a very fast algorithm exists to compute the number of objects or components.
The Euler number is a topological parameter, which describes the structure of an object, regardless of its specific geometric shape. Other topological parameters exist, such as the number of branches or of triple points in a skeleton, the hierarchical degree of a tree-like skeleton or the number of neighbors for a cell in a skeleton by zone of influence.
The connectivity number
can be interpreted geometrically (Euler-Poincaré). The connectivity numbers
,
,
are computed recursively when the spatial dimension increases. Details of this approach are beyond the scope of this documentation.
The Euler number is obtained as the sum of measures in local neighborhoods. In the continuous case, this measure is null almost everywhere, except on contours. An example illustrates this for polygonal shapes in the figure 1.
In the discrete case, the local measure, a search for specific configurations, is derived from the Euler formula for graph:
, where
is the number of connected components,
the number of holes,
the number of vertices,
the number of elementary faces, and
the number of sides.
On a square grid, one gets:
For example, consider the Euler number in the following continuous case of a polygonal object with no loops, and bounding an object or a hole.
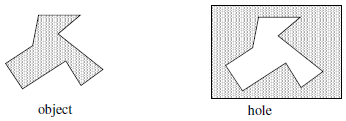
Figure 1: Polygonal object A simple local measure can identify this contour as the boundary of an object or a hole. We define a measure
for each point
in the plane as:
ifis a vertex then the value of
is 0.
Otherwise, consider the side normals.Two situations may occur: the object points (shaded set) lie in the concavity or in the convexity.

Figure 2: Concavity and convexity In the first case the measure
will be defined as:
,
and in the second case as:,
whereis the angle, lying between 0 and
, of the
and
side normals, oriented toward the convexity.
The polygonal measure is then defined as:
One can easily show that:
if P is an object, and:
if P is a hole.
If several disjointed polygonal contours exist in an image, one can apply this measure on each contour, and obtain:
which gives the Euler formula. See also: Average Object Area Per Slice, Volume Fraction, Object Boundary Area, Total Image Boundary Area, Average Object Number Per Slice.
Input Image [required]
The image to be analyzed. Supported types include: binary images (Uniform Label Field with 2 labels).
Interpretation
This port specifies whether the input will be interpreted as a 3D volume or a stack of 2D images for processing.