Description
For introduction please refer to Moments Of Inertia and Moments Of Inertia 3D.
The covariance matrix (or variance-covariance matrix) can be written as:
The orientation is defined as the direction of its major inertia axis. It is given as the eigenvector of the largest eigenvalue of the covariance matrix.
This is a good measure of the orientation for simple, roughly convex objects.
The result 
falls between -180 and +180 degree.
The result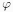 
falls between 0 and 90 degree.
| Figure 1: Figure 1: Azimuthal and polar angles |
The secondary orientation (or orientation2) is defined as the direction of its minor inertia axis. It is given as the eigenvector of the smallest eigenvalue of the covariance matrix.
Extent values
The extent of the data can be computed in the direction of the largest, medium, and smallest eigenvectors of the covariance matrix. These values indicate the extents of the bounding box of the shape oriented along the corresponding eigenvector, with respect to the BaryCenter.
The sums of each minimal and a maximal extents give the sizes of the enclosing bounding box.