Documentation

Tutorial for the Optimization Toolbox™

Open This ExampleOpen This Example

This example shows how to use two nonlinear optimization solvers and how to set options. The nonlinear solvers that we use in this example are fminunc and fmincon.

All the principles outlined in this example apply to the other nonlinear solvers, such as fgoalattain, fminimax, lsqnonlin, lsqcurvefit, and fsolve.

The example starts with minimizing an objective function, then proceeds to minimize the same function with additional parameters. After that, the example shows how to minimize the objective function when there is a constraint, and finally shows how to get a more efficient and/or accurate solution by providing gradients or Hessian, or by changing some options.

Unconstrained Optimization Example

Consider the problem of finding a minimum of the function:

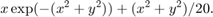
$$x\exp(-(x^2+y^2))+(x^2+y^2)/20.$$

Plot the function to get an idea of where it is minimized

f = @(x,y) x.*exp(-x.^2-y.^2)+(x.^2+y.^2)/20;
ezsurfc(f,[-2,2])

The plot shows that the minimum is near the point (-1/2,0).

Usually you define the objective function as a MATLAB file. For now, this function is simple enough to define as an anonymous function:

fun = @(x) f(x(1),x(2));

Take a guess at the solution:

x0 = [-.5; 0];

Set optimization options to not use fminunc's default large-scale algorithm, since that algorithm requires the objective function gradient to be provided:

options = optimoptions('fminunc','Algorithm','quasi-newton');

View the iterations as the solver calculates:

options.Display = 'iter';

Call fminunc, an unconstrained nonlinear minimizer:

[x, fval, exitflag, output] = fminunc(fun,x0,options);

                                                        First-order 
 Iteration  Func-count       f(x)        Step-size       optimality
     0           3          -0.3769                         0.339
     1           6        -0.379694              1          0.286  
     2           9        -0.405023              1         0.0284  
     3          12        -0.405233              1        0.00386  
     4          15        -0.405237              1       3.17e-05  
     5          18        -0.405237              1       3.35e-08  

Local minimum found.

Optimization completed because the size of the gradient is less than
the default value of the function tolerance.

The solver found a solution at:

uncx = x

uncx =

   -0.6691
    0.0000

The function value at the solution is:

uncf = fval

uncf =

   -0.4052

We will use the number of function evaluations as a measure of efficiency in this example. The total number of function evaluations is:

output.funcCount

ans =

    18

Unconstrained Optimization with Additional Parameters

We will now pass extra parameters as additional arguments to the objective function. We show two different ways of doing this - using a MATLAB file, or using a nested function.

Consider the objective function from the previous section:

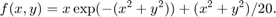
$$f(x,y) = x\exp(-(x^2+y^2))+(x^2+y^2)/20.$$

We parameterize the function with (a,b,c) in the following way:

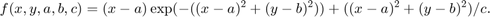
$$f(x,y,a,b,c) = (x-a)\exp(-((x-a)^2+(y-b)^2))+((x-a)^2+(y-b)^2)/c.$$

This function is a shifted and scaled version of the original objective function.

Method 1: MATLAB file Function

Suppose we have a MATLAB file objective function called bowlpeakfun defined as:

type bowlpeakfun

function y = bowlpeakfun(x, a, b, c)
%BOWLPEAKFUN Objective function for parameter passing in TUTDEMO.

%   Copyright 2008 The MathWorks, Inc.

y = (x(1)-a).*exp(-((x(1)-a).^2+(x(2)-b).^2))+((x(1)-a).^2+(x(2)-b).^2)/c;

Define the parameters:

a = 2;
b = 3;
c = 10;

Create an anonymous function handle to the MATLAB file:

f = @(x)bowlpeakfun(x,a,b,c)

f = 

    @(x)bowlpeakfun(x,a,b,c)

Call fminunc to find the minimum:

x0 = [-.5; 0];
options = optimoptions('fminunc','Algorithm','quasi-newton');
[x, fval] = fminunc(f,x0,options)

Local minimum found.

Optimization completed because the size of the gradient is less than
the default value of the function tolerance.




x =

    1.3639
    3.0000


fval =

   -0.3840

Method 2: Nested Function

Consider the following function that implements the objective as a nested function

type nestedbowlpeak

function [x,fval] =  nestedbowlpeak(a,b,c,x0,options)
%NESTEDBOWLPEAK Nested function for parameter passing in TUTDEMO.

%   Copyright 2008 The MathWorks, Inc.

[x,fval] = fminunc(@nestedfun,x0,options);  
    function y = nestedfun(x)
      y = (x(1)-a).*exp(-((x(1)-a).^2+(x(2)-b).^2))+((x(1)-a).^2+(x(2)-b).^2)/c;    
    end
end

In this method, the parameters (a,b,c) are visible to the nested objective function called nestedfun. The outer function, nestedbowlpeak, calls fminunc and passes the objective function, nestedfun.

Define the parameters, initial guess, and options:

a = 2;
b = 3;
c = 10;
x0 = [-.5; 0];
options = optimoptions('fminunc','Algorithm','quasi-newton');

Run the optimization:

[x,fval] =  nestedbowlpeak(a,b,c,x0,options)

Local minimum found.

Optimization completed because the size of the gradient is less than
the default value of the function tolerance.




x =

    1.3639
    3.0000


fval =

   -0.3840

You can see both methods produced identical answers, so use whichever one you find most convenient.

Constrained Optimization Example: Inequalities

Consider the above problem with a constraint:

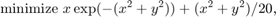
$$\mbox{minimize }x\exp(-(x^2+y^2))+(x^2+y^2)/20,$$

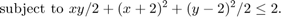
$$\mbox{subject to }xy/2 + (x+2)^2 + (y-2)^2/2 \le 2.$$

The constraint set is the interior of a tilted ellipse. Look at the contours of the objective function plotted together with the tilted ellipse

f = @(x,y) x.*exp(-x.^2-y.^2)+(x.^2+y.^2)/20;
g = @(x,y) x.*y/2+(x+2).^2+(y-2).^2/2-2;
ezplot(g,[-6,0,-1,7])
hold on
ezcontour(f,[-6,0,-1,7])
plot(-.9727,.4685,'ro');
legend('constraint','f contours','minimum');
hold off

The plot shows that the lowest value of the objective function within the ellipse occurs near the lower right part of the ellipse. We are about to calculate the minimum that was just plotted. Take a guess at the solution:

x0 = [-2 1];

Set optimization options: use the interior-point algorithm, and turn on the display of results at each iteration:

options = optimoptions('fmincon','Algorithm','interior-point','Display','iter');

Solvers require that nonlinear constraint functions give two outputs: one for nonlinear inequalities, the second for nonlinear equalities. So we write the constraint using the deal function to give both outputs:

gfun = @(x) deal(g(x(1),x(2)),[]);

Call the nonlinear constrained solver. There are no linear equalities or inequalities or bounds, so pass [ ] for those arguments:

[x,fval,exitflag,output] = fmincon(fun,x0,[],[],[],[],[],[],gfun,options);

                                            First-order      Norm of
 Iter F-count            f(x)  Feasibility   optimality         step
    0       3    2.365241e-01    0.000e+00    1.972e-01
    1       6    1.748504e-01    0.000e+00    1.734e-01    2.260e-01
    2      10   -1.570560e-01    0.000e+00    2.608e-01    9.347e-01
    3      14   -6.629160e-02    0.000e+00    1.241e-01    3.103e-01
    4      17   -1.584082e-01    0.000e+00    7.934e-02    1.826e-01
    5      20   -2.349124e-01    0.000e+00    1.912e-02    1.571e-01
    6      23   -2.255299e-01    0.000e+00    1.955e-02    1.993e-02
    7      26   -2.444225e-01    0.000e+00    4.293e-03    3.821e-02
    8      29   -2.446931e-01    0.000e+00    8.100e-04    4.035e-03
    9      32   -2.446933e-01    0.000e+00    1.999e-04    8.126e-04
   10      35   -2.448531e-01    0.000e+00    4.004e-05    3.289e-04
   11      38   -2.448927e-01    0.000e+00    4.036e-07    8.156e-05

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.

A solution to this problem has been found at:

x

x =

   -0.9727    0.4686

The function value at the solution is:

fval

fval =

   -0.2449

The total number of function evaluations was:

Fevals = output.funcCount

Fevals =

    38

The inequality constraint is satisfied at the solution.

[c, ceq] = gfun(x)

c =

  -2.4608e-06


ceq =

     []

Since c(x) is close to 0, the constraint is "active," meaning the constraint affects the solution. Recall the unconstrained solution was found at

uncx

uncx =

   -0.6691
    0.0000

and the unconstrained objective function was found to be

uncf

uncf =

   -0.4052

The constraint moved the solution, and increased the objective by

fval-uncf

ans =

    0.1603

Constrained Optimization Example: User-Supplied Gradients

Optimization problems can be solved more efficiently and accurately if gradients are supplied by the user. This example shows how this may be performed. We again solve the inequality-constrained problem

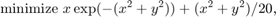
$$\mbox{minimize }x\exp(-(x^2+y^2))+(x^2+y^2)/20,$$

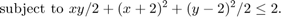
$$\mbox{subject to }xy/2 + (x+2)^2 + (y-2)^2/2 \le 2.$$

To provide the gradient of f(x) to fmincon, we write the objective function in the form of a MATLAB file:

type onehump

function [f,gf] = onehump(x)
% ONEHUMP Helper function for Tutorial for the Optimization Toolbox demo

%   Copyright 2008-2009 The MathWorks, Inc.

r = x(1)^2 + x(2)^2;
s = exp(-r);
f = x(1)*s+r/20;

if nargout > 1
   gf = [(1-2*x(1)^2)*s+x(1)/10;
       -2*x(1)*x(2)*s+x(2)/10];
end

The constraint and its gradient are contained in the MATLAB file tiltellipse:

type tiltellipse

function [c,ceq,gc,gceq] = tiltellipse(x)
% TILTELLIPSE Helper function for Tutorial for the Optimization Toolbox demo

%   Copyright 2008-2009 The MathWorks, Inc.

c = x(1)*x(2)/2 + (x(1)+2)^2 + (x(2)-2)^2/2 - 2;
ceq = [];

if nargout > 2
   gc = [x(2)/2+2*(x(1)+2);
       x(1)/2+x(2)-2];
   gceq = [];
end

Make a guess at the solution:

x0 = [-2; 1];

Set optimization options: we continue to use the same algorithm for comparison purposes.

options = optimoptions('fmincon','Algorithm','interior-point');

We also set options to use the gradient information in the objective and constraint functions. Note: these options MUST be turned on or the gradient information will be ignored.

options = optimoptions(options,'GradObj','on','GradConstr','on');

There should be fewer function counts this time, since fmincon does not need to estimate gradients using finite differences.

options.Display = 'iter';

Call the solver:

[x,fval,exitflag,output] = fmincon(@onehump,x0,[],[],[],[],[],[], ...
                                   @tiltellipse,options);

                                            First-order      Norm of
 Iter F-count            f(x)  Feasibility   optimality         step
    0       1    2.365241e-01    0.000e+00    1.972e-01
    1       2    1.748504e-01    0.000e+00    1.734e-01    2.260e-01
    2       4   -1.570560e-01    0.000e+00    2.608e-01    9.347e-01
    3       6   -6.629161e-02    0.000e+00    1.241e-01    3.103e-01
    4       7   -1.584082e-01    0.000e+00    7.934e-02    1.826e-01
    5       8   -2.349124e-01    0.000e+00    1.912e-02    1.571e-01
    6       9   -2.255299e-01    0.000e+00    1.955e-02    1.993e-02
    7      10   -2.444225e-01    0.000e+00    4.293e-03    3.821e-02
    8      11   -2.446931e-01    0.000e+00    8.100e-04    4.035e-03
    9      12   -2.446933e-01    0.000e+00    1.999e-04    8.126e-04
   10      13   -2.448531e-01    0.000e+00    4.004e-05    3.289e-04
   11      14   -2.448927e-01    0.000e+00    4.036e-07    8.156e-05

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.

fmincon estimated gradients well in the previous example, so the iterations in the current example are similar.

The solution to this problem has been found at:

xold = x

xold =

   -0.9727
    0.4686

The function value at the solution is:

minfval = fval

minfval =

   -0.2449

The total number of function evaluations was:

Fgradevals = output.funcCount

Fgradevals =

    14

Compare this to the number of function evaluations without gradients:

Fevals

Fevals =

    38

Changing the Default Termination Tolerances

This time we solve the same constrained problem

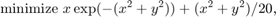
$$\mbox{minimize }x\exp(-(x^2+y^2))+(x^2+y^2)/20,$$

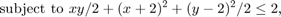
$$\mbox{subject to }xy/2 + (x+2)^2 + (y-2)^2/2 \le 2,$$

more accurately by overriding the default termination criteria (options.TolX and options.TolFun). We continue to use gradients. The default values for fmincon's interior-point algorithm are options.TolX = 1e-10, options.TolFun = 1e-6.

Override two default termination criteria: termination tolerances on X and fval.

options = optimoptions(options,'TolX',1e-15,'TolFun',1e-8);

Call the solver:

[x,fval,exitflag,output] = fmincon(@onehump,x0,[],[],[],[],[],[], ...
                                   @tiltellipse,options);

                                            First-order      Norm of
 Iter F-count            f(x)  Feasibility   optimality         step
    0       1    2.365241e-01    0.000e+00    1.972e-01
    1       2    1.748504e-01    0.000e+00    1.734e-01    2.260e-01
    2       4   -1.570560e-01    0.000e+00    2.608e-01    9.347e-01
    3       6   -6.629161e-02    0.000e+00    1.241e-01    3.103e-01
    4       7   -1.584082e-01    0.000e+00    7.934e-02    1.826e-01
    5       8   -2.349124e-01    0.000e+00    1.912e-02    1.571e-01
    6       9   -2.255299e-01    0.000e+00    1.955e-02    1.993e-02
    7      10   -2.444225e-01    0.000e+00    4.293e-03    3.821e-02
    8      11   -2.446931e-01    0.000e+00    8.100e-04    4.035e-03
    9      12   -2.446933e-01    0.000e+00    1.999e-04    8.126e-04
   10      13   -2.448531e-01    0.000e+00    4.004e-05    3.289e-04
   11      14   -2.448927e-01    0.000e+00    4.036e-07    8.156e-05
   12      15   -2.448931e-01    0.000e+00    4.000e-09    8.230e-07

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the selected value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.

We now choose to see more decimals in the solution, in order to see more accurately the difference that the new tolerances make.

format long

The optimizer found a solution at:

x

x =

  -0.972742227363546
   0.468569289098342

Compare this to the previous value:

xold

xold =

  -0.972742694488360
   0.468569966693330

The change is

x - xold

ans =

   1.0e-06 *

   0.467124813385844
  -0.677594988729435

The function value at the solution is:

fval

fval =

  -0.244893137879894

The solution improved by

fval - minfval

ans =

    -3.996450220755676e-07

(this is negative since the new solution is smaller)

The total number of function evaluations was:

output.funcCount

ans =

    15

Compare this to the number of function evaluations when the problem is solved with user-provided gradients but with the default tolerances:

Fgradevals

Fgradevals =

    14

Constrained Optimization Example with User-Supplied Hessian

If you give not only a gradient, but also a Hessian, solvers are even more accurate and efficient.

fmincon's interior-point solver takes a Hessian matrix as a separate function (not part of the objective function). The Hessian function H(x,lambda) should evaluate the Hessian of the Lagrangian; see the User's Guide for the definition of this term.

Solvers calculate the values lambda.ineqnonlin and lambda.eqlin; your Hessian function tells solvers how to use these values.

In this problem we have but one inequality constraint, so the Hessian is:

type hessfordemo

function H = hessfordemo(x,lambda)
% HESSFORDEMO Helper function for Tutorial for the Optimization Toolbox demo

%   Copyright 2008-2009 The MathWorks, Inc.

s = exp(-(x(1)^2+x(2)^2));
H = [2*x(1)*(2*x(1)^2-3)*s+1/10, 2*x(2)*(2*x(1)^2-1)*s;
        2*x(2)*(2*x(1)^2-1)*s, 2*x(1)*(2*x(2)^2-1)*s+1/10];
hessc = [2,1/2;1/2,1];
H = H + lambda.ineqnonlin(1)*hessc;

In order to use the Hessian, you need to set options appropriately:

options = optimoptions('fmincon','Algorithm','interior-point','GradConstr','on',...
    'GradObj','on','Hessian','user-supplied','HessFcn',@hessfordemo);

The tolerances have been set back to the defaults. There should be fewer function counts this time.

options.Display = 'iter';

Call the solver:

[x,fval,exitflag,output] = fmincon(@onehump,x0,[],[],[],[],[],[], ...
                                   @tiltellipse,options);

                                            First-order      Norm of
 Iter F-count            f(x)  Feasibility   optimality         step
    0       1    2.365241e-01    0.000e+00    1.972e-01
    1       3    5.821325e-02    0.000e+00    1.443e-01    8.728e-01
    2       5   -1.218829e-01    0.000e+00    1.007e-01    4.927e-01
    3       6   -1.421167e-01    0.000e+00    8.486e-02    5.165e-02
    4       7   -2.261916e-01    0.000e+00    1.989e-02    1.667e-01
    5       8   -2.433609e-01    0.000e+00    1.537e-03    3.486e-02
    6       9   -2.446875e-01    0.000e+00    2.057e-04    2.727e-03
    7      10   -2.448911e-01    0.000e+00    2.068e-06    4.191e-04
    8      11   -2.448931e-01    0.000e+00    2.001e-08    4.218e-06

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.

There were fewer, and different iterations this time.

The solution to this problem has been found at:

x

x =

  -0.972742246093537
   0.468569316215571

The function value at the solution is:

fval

fval =

  -0.244893121872758

The total number of function evaluations was:

output.funcCount

ans =

    11

Compare this to the number using only gradient evaluations, with the same default tolerances:

Fgradevals

Fgradevals =

    14
Was this topic helpful?
Optimization Toolbox Documentation
Other Documentation
Support