Documentation

This example shows the value of using sparse arithmetic when you have a sparse problem. The matrix has n rows, where you choose n to be a large value. A full matrix of size n-by-n can use up all available memory, but a sparse matrix presents no problem.

The problem is to minimize x'*H*x/2 + f'*x subject to

x(1) + x(2) + ... + x(n) = 0,

where f = [-1;-2;-3;...;-n].

1. Create the parameter n and the utility matrix T. The matrix T is a sparse circulant matrix that is simply a helper for creating the sparse positive-definite quadratic matrix H.

   n = 30000; % Adjust n to a large value
   T = spalloc(n,n,n); % make a sparse circulant matrix
   r = 1:n-1;
   for m = r
       T(m,m+1)=1;
   end
   T(n,1) = 1;

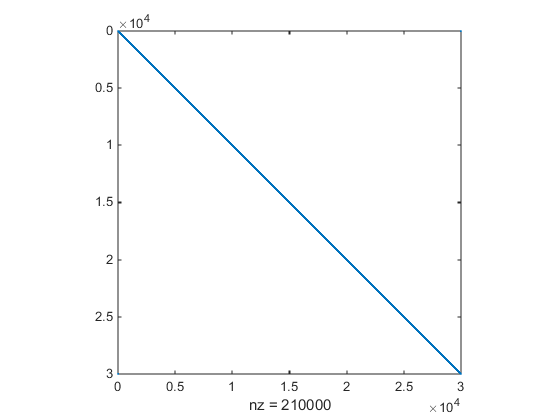
2. Create a sparse vector v. Then create the matrix H by shifted versions of v*v'. The matrix T creates shifts of v.

   v(n) = 0; v(1) = 1; v(2) = 2; v(4) = 3;
   v = (sparse(v))';
   % Make a banded type of matrix
   H = spalloc(n,n,7*n);
   r = 1:n;
   for m = r
       H = H + v*v';
       v = T*v;
   end

3. Take a look at the structure of H:

   spy(H)

   

4. Create the problem vector f and linear constraint.

   f = -r; % linear term
   A = ones(1,n); b = 0;

5. Solve the quadratic programming problem with the interior-point-convex algorithm.

   options = optimoptions(@quadprog,'Algorithm','interior-point-convex');
   [x,fval,exitflag,output,lambda] = ...
       quadprog(H,f,A,b,[],[],[],[],[],options);
   
   Minimum found that satisfies the constraints.
   Optimization completed because the objective function is 
   non-decreasing in feasible directions, to within the selected
   value of the function tolerance, and constraints are satisfied 
   to within the selected value of the constraint tolerance.

6. View the solution value, output structure, and Lagrange multiplier:

   fval,output,lambda
   
   fval =
    -3.1331e+10
   
   output = 
                   message: 'Minimum found that satisfies the constraints.…'
                 algorithm: 'interior-point-convex'
             firstorderopt: 1.1665e-04
           constrviolation: 7.7762e-09
                iterations: 6
              cgiterations: []
   
   lambda = 
       ineqlin: 1.5000e+004
         eqlin: [0x1 double]
         lower: [30000x1 double]
         upper: [30000x1 double]

   Since there are no lower bounds or upper bounds, all the values in lambda.lower and lambda.upper are 0. The inequality constraint is active, since lambda.ineqlin is nonzero.

7. On many computers you cannot create a full n-by-n matrix when n = 30000. So you can run this problem only using sparse matrices.

   H2 = zeros(3e4);

   Out of memory. Type HELP MEMORY for your options.