


Automatic recognition (graph labelling) using a model
Warning: in BrainVISA version 4.1 and later, new recognition models are available (2011 variants), which follow the same nomenclature and learning database as the SPAM models, but slightly differ from the older 2000-2001 models. the new models are used by default, but the older ones are still available.
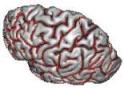
This procedure gives automatically a name to each elementary cortical fold provided by Ana Compute Cortical Fold Arg. Example of result :
The list of names used (standard nomenclature, sulcal roots, etc.) depends on the application. The sulcus recognition method relies on a congregation of virtual local experts, each expert being in charge of one given anatomical feature. These experts have been trained on a database of brains, whose sulci have been manually identified by our human anatomist. If you wish to obtain your own anatomical definitions, you may provide another database of labelled brains. Then, we will train another congregation which will mimic your labelling.
The sulcus recognition amounts to the search for the labelling which maximizes the consensus among the expert assembly. Each expert is a small artificial neural network called multilayer perceptron. Two families of such networks are used. One is in charge of the shapes of the sulci. The second one is in charge of the shapes made up by two neighboring sulci. Hence, the identification of one given sulcus depends on the opinion of several local experts: one in charge of the sulcus shape and a set of neigbor's experts in charge of the surrounding patterns. This contextual approach can lead to correct labelling even if some experts are wrong. Some analogy with biological models of vision could be discussed. One expert could be viewed as a cortical column, while the congregation has a "corticotopic" organization....
The sulcus patterns have to be traduced before being presented to neural networks. This traduction converts the pattern to a code made up of various morphometry-like parameters (size, orientation in Talairach space, depth, number of connected component, etc.).
The training of one given expert consists in presenting alternatively correct and non correct examples of the pattern that has to be learned. The network is supervised during this learning. Little by little, the network learns to provide a low answer (around zero) for correct examples, and a high answer (around 1) for non correct ones. To check if the network can generalize this knowledge, a second learning database is used. This checking is performed from time to time during the learning and leads to stop it when the network begins to learn the first database by heart. Otherwise, the network would lose generalization capacity.
the charts above give a few examples of the evolution of the mean error during the learning. When the sulcus shape is simple like for central sulcus, the learning is fast and the generalization almost perfect. When the pattern to be learned is more variable, like for intermediate precentral sulcus, the generalization does not work for each example. In such cases, the networks in charge of the surrounding patterns will provide more knowledge to the system.
At the end of the learning phase, the reliability of each expert is evaluated on the second base. Some turn out to be very bad, because they were given a job without solution. To deal with this situation, the contribution of a given expert to the global congregation is weighted by its reliability.
The search for the best consensus among the congregation is difficult. The weighted sum of the expert's opinions has to be minimized. Unfortunately, the landscape corresponding to this sum has a lot of local minima without interest. In order to find a way to the deep valley including the best solution, we used an idea stemming from the field of glass design. Sorry, some more translation to be done, I am going back home now:-) Le modèle sous-jacent à l'assemblée d'experts locaux est en effet inspiré de la physique des verres de spins. La minimisation est conduite à partir d'une technique appelée recuit simulé. Elle correspond à une réalité dans le monde des verres: pour obtenir des cristaux avec peu de défauts, il faut d'abord les chauffer puis les refroidir très lentement. C'est ce qui permet au verre de trouver un état d'énergie très faible, correspondant à l'absence de défauts. L'agitation liée à la température lui permet de franchir les petites barrières de potentiel qui entourent les minima locaux correspondant à des défauts. Au fur à mesure que la température baisse, il est de plus en plus difficile de sortir de ces cul-de-sac.
Si on revient à l'idée d'un paysage de montagne, on peut imaginer un promeneur perdu dans le brouillard qui cherche à retourner à la station située dans la vallée la plus profonde. S'il se contente de descendre la pente où il se trouve, il va vite se retrouver bloqué au fond d'une combe. Dans la réalité, pendant un certain temps, il sortira des petits vallons en espérant en trouver un autre plus profond à coté donnant sur la station. Mais, petit à petit, la fatigue le gagnant, il ne sera plus capable de remonter les parois les plus abruptes. Il finira par se trouver bloqué au fond d'une vallée profonde. S'il a de la chance, il s'agira de la station...
L'évolution de l'énergie correspondant à notre modèle pendant le recuit simulé est la suivante:
Pendant un certain temps, la température est élévée et l'étiquetage évolue de manière quasi-aléatoire. Puis apparait une transition correspondant pratiquement à l'identification des grands sillons. L'énergie chute rapidement. Enfin, une propagation plus lente aux sillons de moindre importance amène au fond de la vallée. Comme le montre l'analogie du promeneur, le recuit simulé est une approche stochastique qui peut parfois échouer. Il est donc prudent de réaliser plusieurs tirages et de choisir celui qui est arrivé le plus bas. Nous avons vérifié à de nombreuses reprises que cette heuristique maximisait l'adéquation avec une identification manuelle. Voici un exemple où 10 recuits différents ont été réalisés sur le même cerveau :
Accord avec l'expert humain en fonction de l'énergie finale :
En fait, comme on ne connait pas actuellement la solution idéale au problème de l'identification des sillons, il n'est guère possible d'espérer un accord parfait entre l'expert humain et notre système. Il n'est donc pas nécessaire de faire énormément de tirages pour obtenir une solution raisonnable à tous les coups...
Pour finir, il est intéressant, pour comprendre notre approche, de faire un parallèle avec la méthode concurrente qui consiste à déformer une image modèle dont les sillons ont été identifiés. Dans ce dernier cas, seules les intensités guident les déformations, ce qui conduit parfois à apparier des sillons différents. En fait, la méthode fondée sur des déformations est trop couteuse pour permettre une minimisation de type recuit simulé. On peut donc interpréter des erreurs d'appariement entre sillons comme un blocage dans une vallée pas suffisamment profonde. Notre approche qui travaille à un niveau plus élévé de représentation des formes permet de résoudre ces problèmes. Le modèle n'est plus une image mais une structure probabiliste de type graphe. Les déformations sont remplacées par un étiquetage, ce qui revient à apparier le graphe modèle avec le graphe représentant le nouveau cerveau.
La notion de graphe aléatoire:
Pour plus d'information :
A Markovian random field based random graph modelling the human cortical topography, J.-F. Mangin, J. Régis, I. Bloch, V. Frouin, Y. Samson, and J. Lopez-Krahe In CVRMed, Nice, LNCS-905, Springer-Verlag, pages 177--183, 1995.
Automatic recognition of cortical sulci of the human brain using a congregation of neural networks. D. Rivière, J.-F. Mangin, D. Papadopoulos, J.-M. Martinez, V. Frouin, and J. Régis. Medical Image Analysis, 6(2), pp 77-92
Pour une approche combinant reconnaissance des sillons et déformations non rigides développée avec le projet Epidaure de l'INRIA:
Multisubject non-rigid registration of brain MRI using intensity and geometric features. P. Cachier, J.-F. Mangin, X. Pennec, D. Rivière, D. Papadopoulos-Orfanos, J. Régis, and N. Ayache. In MICCAI, Utrecht, The Netherlands, LNCS-2208, Springer Verlag, pages 734--742, 2002.
data_graph: Data graph ( input )
Data to be labelled
model: Model graph ( input )Model graph (knowledge)
output_graph: Labelled Cortical folds graph ( output )Output graph (labelled)
model_hint: Choice ( input )
energy_plot_file: siRelax Fold Energy ( output )
rate: Float ( input )
stopRate: Float ( input )
niterBelowStopProp: Integer ( input )
forbid_unknown_label: Boolean ( input )
Toolbox : Morphologist
User level : 0
Identifier :
recognitionFile name :
brainvisa/toolboxes/morphologist/processes/Sulci/Recognition/recognition.pySupported file formats :
data_graph :Graph and datamodel :Graph and dataoutput_graph :Graph and dataenergy_plot_file :siRelax Fold Energy