Documentation

fzero

Root of nonlinear function

collapse all in page

Syntax

  • [x,fval,exitflag,output] = fzero(___)
    example

Description

example

x = fzero(fun,x0) tries to find a point x where fun(x) = 0. This solution is where fun(x) changes sign—fzero cannot find a root of a function such as x^2.

example

x = fzero(fun,x0,options) uses options to modify the solution process.

example

x = fzero(problem) solves a root-finding problem specified by problem.

example

[x,fval,exitflag,output] = fzero(___) returns fun(x) in the fval output, exitflag encoding the reason fzero stopped, and an output structure containing information on the solution process.

Examples

collapse all

Root Starting From One Point

Calculate $\pi$ by finding the zero of the sine function near 3.

fun = @sin; % function
x0 = 3; % initial point
x = fzero(fun,x0)

x =

    3.1416

Root Starting From an Interval

Find the zero of cosine between 1 and 2.

fun = @cos; % function
x0 = [1 2]; % initial interval
x = fzero(fun,x0)

x =

    1.5708

Note that cos(1) and cos(2) differ in sign.

Root of a Function Defined by a File

Find a zero of the function f(x) = x3 – 2x – 5.

First, write a file called f.m.

function y = f(x)
y = x.^3-2*x-5;

Save f.m on your MATLAB® path.

Find the zero of f(x) near 2.

fun = @f; % function
x0 = 2; % initial point
z = fzero(fun,x0)
z =
    2.0946

Since f(x) is a polynomial, you can find the same real zero, and a complex conjugate pair of zeros, using the roots command.

roots([1 0 -2 -5])
   ans =
   2.0946          
  -1.0473 + 1.1359i
  -1.0473 - 1.1359i

Root of Function with Extra Parameter

Find the root of a function that has an extra parameter.

myfun = @(x,c) cos(c*x);  % parameterized function
c = 2;                    % parameter
fun = @(x) myfun(x,c);    % function of x alone
x = fzero(fun,0.1)

x =

    0.7854

Nondefault Options

Plot the solution process by setting some plot functions.

Define the function and initial point.

fun = @(x)sin(cosh(x));
x0 = 1;

Examine the solution process by setting options that include plot functions.

options = optimset('PlotFcns',{@optimplotx,@optimplotfval});

Run fzero including options.

x = fzero(fun,x0,options)

x =

    1.8115

Solve Exported Problem

Solve a problem that is defined by an export from Optimization app.

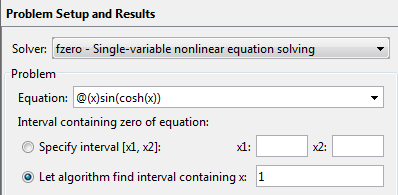
Define a problem in Optimization app. Enter optimtool('fzero'), and fill in the problem as pictured.

    Note:   The Optimization app warns that it will be removed in a future release.

Select File > Export to Workspace, and export the problem as pictured to a variable named problem.

Enter the following at the command line.

x = fzero(problem)
x =

    1.8115

More Information from Solution

Find the point where exp(-exp(-x)) = x, and display information about the solution process.

fun = @(x) exp(-exp(-x)) - x; % function
x0 = [0,1]; % initial interval
options = optimset('Display','iter'); % show iterations
[x,fval,exitflag,output] = fzero(fun,x0,options)

 
 Func-count    x          f(x)             Procedure
    2               1     -0.307799        initial
    3        0.544459     0.0153522        interpolation
    4        0.566101    0.00070708        interpolation
    5        0.567143  -1.40255e-08        interpolation
    6        0.567143   1.50013e-12        interpolation
    7        0.567143             0        interpolation
 
Zero found in the interval [0, 1]

x =

    0.5671


fval =

     0


exitflag =

     1


output = 

    intervaliterations: 0
            iterations: 5
             funcCount: 7
             algorithm: 'bisection, interpolation'
               message: 'Zero found in the interval [0, 1]'

fval = 0 means fun(x) = 0, as desired.

Related Examples

Input Arguments

collapse all

fun — Function to solvefunction handle

Function to solve, specified as a handle to a scalar-valued function. fun accepts a scalar x and returns a scalar fun(x).

fzero solves fun(x) = 0. To solve an equation fun(x) = c(x), instead solve fun2(x) = fun(x) - c(x) = 0.

To include extra parameters in your function, see the example Root of Function with Extra Parameter and the section Passing Extra Parameters.

Example: @sin

Example: @myFunction

Example: @(x)(x-a)^5 - 3*x + a - 1

Data Types: function_handle

x0 — Initial valuescalar | 2-element vector

Initial value, specified as a real scalar or a 2-element real vector.

  • Scalar — fzero begins at x0 and tries to locate a point x1 where fun(x1) has the opposite sign of fun(x0). Then fzero iteratively shrinks the interval where fun changes sign to reach a solution.

  • 2-element vector — fzero checks that fun(x0(1)) and fun(x0(2)) have opposite signs, and errors if they do not. It then iteratively shrinks the interval where fun changes sign to reach a solution. An interval x0 must be finite; it cannot contain ±Inf.

    Tip   Calling fzero with an interval (x0 with two elements) is often faster than calling it with a scalar x0.

Example: 3

Example: [2,17]

Data Types: double

options — Options for solution processstructure, typically created using optimset

Options for solution process, specified as a structure. Create or modify the options structure using optimset. fzero uses these options structure fields.

Display

Level of display (see Iterative Display):

  • 'off' displays no output.

  • 'iter' displays output at each iteration.

  • 'final' displays just the final output.

  • 'notify' (default) displays output only if the function does not converge.

FunValCheck

Check whether objective function values are valid.

  • 'on' displays an error when the objective function returns a value that is complex, Inf, or NaN.

  • The default, 'off', displays no error.

OutputFcn

Specify one or more user-defined functions that an optimization function calls at each iteration, either as a function handle or as a cell array of function handles. The default is none ([]). See Output Function.

PlotFcns

Plot various measures of progress while the algorithm executes. Select from predefined plots or write your own. Pass a function handle or a cell array of function handles. The default is none ([]).

  • @optimplotx plots the current point.

  • @optimplotfval plots the function value.

For information on writing a custom plot function, see Plot Functions.

TolX

Termination tolerance on x, a positive scalar. The default is eps, 2.2204e–16. See Tolerances and Stopping Criteria.

Example: options = optimset('FunValCheck','on')

Data Types: struct

problem — Root-finding problemstructure

Root-finding problem, specified as a structure with all of the following fields.

objective

Objective function

x0

Initial point for x, scalar or 2-D vector

solver

'fzero'

options

Options structure, typically created using optimset

You can generate problem by exporting from Optimization app. See Importing and Exporting Your Work or Solve Exported Problem.

Data Types: struct

Output Arguments

collapse all

x — Location of root or sign changereal scalar

Location of root or sign change, returned as a scalar.

fval — Function value at xreal scalar

Function value at x, returned as a scalar.

exitflag — Integer encoding the exit conditioninteger

Integer encoding the exit condition, meaning the reason fzero stopped its iterations.

1

Function converged to a solution x.

-1

Algorithm was terminated by the output function or plot function.

-3

NaN or Inf function value was encountered while searching for an interval containing a sign change.

-4

Complex function value was encountered while searching for an interval containing a sign change.

-5

Algorithm might have converged to a singular point.

-6

fzero did not detect a sign change.

output — Information about root-finding processstructure

Information about root-finding process, returned as a structure. The fields of the structure are:

intervaliterations

Number of iterations taken to find an interval containing a root

iterations

Number of zero-finding iterations

funcCount

Number of function evaluations

algorithm

'bisection, interpolation'

message

Exit message

More About

expand all

Algorithms

The fzero command is a function file. The algorithm, created by T. Dekker, uses a combination of bisection, secant, and inverse quadratic interpolation methods. An Algol 60 version, with some improvements, is given in [1]. A Fortran version, upon which fzero is based, is in [2].

References

[1] Brent, R., Algorithms for Minimization Without Derivatives, Prentice-Hall, 1973.

[2] Forsythe, G. E., M. A. Malcolm, and C. B. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, 1976.

See Also

| | | |

Introduced before R2006a

Was this topic helpful?
Optimization Toolbox Documentation
Other Documentation
Support