Documentation

fmincon

Find minimum of constrained nonlinear multivariable function

collapse all in page

Nonlinear programming solver.

Finds the minimum of a problem specified by

minxf(x) such that {c(x)≤0ceq(x)=0A⋅x≤bAeq⋅x=beqlb≤x≤ub,

b and beq are vectors, A and Aeq are matrices, c(x) and ceq(x) are functions that return vectors, and f(x) is a function that returns a scalar. f(x), c(x), and ceq(x) can be nonlinear functions.

x, lb, and ub can be passed as vectors or matrices; see Matrix Arguments.

Syntax

  • x = fmincon(fun,x0,A,b)
    example
  • x = fmincon(fun,x0,A,b,Aeq,beq)
    example
  • x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
    example
  • x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
    example
  • x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
    example
  • x = fmincon(problem)
    example
  • [x,fval] = fmincon(___)
    example
  • [x,fval,exitflag,output] = fmincon(___)
    example
  • [x,fval,exitflag,output,lambda,grad,hessian] = fmincon(___)
    example

Description

example

x = fmincon(fun,x0,A,b) starts at x0 and attempts to find a minimizer x of the function described in fun subject to the linear inequalities A*x ≤ b. x0 can be a scalar, vector, or matrix.

    Note:   Passing Extra Parameters explains how to pass extra parameters to the objective function and nonlinear constraint functions, if necessary.

example

x = fmincon(fun,x0,A,b,Aeq,beq) minimizes fun subject to the linear equalities Aeq*x = beq and A*x ≤ b. If no inequalities exist, set A = [] and b = [].

example

x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub) defines a set of lower and upper bounds on the design variables in x, so that the solution is always in the range lb ≤ x ≤ ub. If no equalities exist, set Aeq = [] and beq = []. If x(i) is unbounded below, set lb(i) = -Inf, and if x(i) is unbounded above, set ub(i) = Inf.

    Note:   If the specified input bounds for a problem are inconsistent, the output x is x0 and the output fval is [].

    Components of x0 that violate the bounds lb ≤ x ≤ ub are reset to the interior of the box defined by the bounds. Components that respect the bounds are not changed. See Iterations Can Violate Constraints.

example

x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon) subjects the minimization to the nonlinear inequalities c(x) or equalities ceq(x) defined in nonlcon. fmincon optimizes such that c(x) ≤ 0 and ceq(x) = 0. If no bounds exist, set lb = [] and/or ub = [].

example

x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options) minimizes with the optimization options specified in options. Use optimoptions to set these options. If there are no nonlinear inequality or equality constraints, set nonlcon = [].

example

x = fmincon(problem) finds the minimum for problem, where problem is a structure described in Input Arguments. Create the problem structure by exporting a problem from Optimization app, as described in Exporting Your Work.

example

[x,fval] = fmincon(___), for any syntax, returns the value of the objective function fun at the solution x.

example

[x,fval,exitflag,output] = fmincon(___) additionally returns a value exitflag that describes the exit condition of fmincon, and a structure output with information about the optimization process.

example

[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(___) additionally returns:

  • lambda — Structure with fields containing the Lagrange multipliers at the solution x.

  • grad — Gradient of fun at the solution x.

  • hessian — Hessian of fun at the solution x. See fmincon Hessian.

Examples

collapse all

Linear Inequality Constraint

Find the minimum value of Rosenbrock's function when there is a linear inequality constraint.

Set the objective function fun to be Rosenbrock's function. Rosenbrock's function is well-known to be difficult to minimize. It has its minimum objective value of 0 at the point (1,1). For more information, see Solve a Constrained Nonlinear Problem.

fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;

Find the minimum value starting from the point [-1,2], constrained to have $x(1) + 2x(2) \le 1$. Express this constraint in the form Ax <= b by taking A = [1,2] and b = 1. Notice that this constraint means that the solution will not be at the unconstrained solution (1,1), because at that point $x(1) + 2x(2) = 3 &gt; 1$.

x0 = [-1,2];
A = [1,2];
b = 1;
x = fmincon(fun,x0,A,b)

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.




x =

    0.5022    0.2489

Linear Inequality and Equality Constraint

Find the minimum value of Rosenbrock's function when there are both a linear inequality constraint and a linear equality constraint.

Set the objective function fun to be Rosenbrock's function.

fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;

Find the minimum value starting from the point [0.5,0], constrained to have $x(1) + 2x(2) \le 1$ and $2x(1) + x(2) = 1$.

  • Express the linear inequality constraint in the form A*x <= b by taking A = [1,2] and b = 1.

  • Express the linear equality constraint in the form Aeq*x <= beq by taking Aeq = [2,1] and beq = 1.

x0 = [0.5,0];
A = [1,2];
b = 1;
Aeq = [2,1];
beq = 1;
x = fmincon(fun,x0,A,b,Aeq,beq)

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.




x =

    0.4149    0.1701

Bound Constraints

Find the minimum of an objective function in the presence of bound constraints.

The objective function is a simple algebraic function of two variables.

fun = @(x)1+x(1)/(1+x(2)) - 3*x(1)*x(2) + x(2)*(1+x(1));

Look in the region where x has positive values, x(1) ≤ 1, and x(2) ≤ 2.

lb = [0,0];
ub = [1,2];

There are no linear constraints, so set those arguments to [].

A = [];
b = [];
Aeq = [];
beq = [];

Try an initial point in the middle of the region. Find the minimum of fun, subject to the bound constraints.

x0 = [0.5,1];
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.

<stopping criteria details>
x =

    1.0000    2.0000
A different initial point can lead to a different solution.
x0 = x0/5;
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.

<stopping criteria details>
x =

   1.0e-06 *

    0.4000    0.4000
To see which solution is better, see Obtain the Objective Function Value.
Nonlinear Constraints



Find the minimum of a function subject to nonlinear constraints



Find the point where Rosenbrock's function is minimized within a circle, also subject to bound constraints.
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;

Look within the region 
$0 \le x(1) \le 0.5$, 
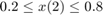$0.2 \le x(2) \le 0.8$.
lb = [0,0.2];
ub = [0.5,0.8];

Also look within the circle centered at [1/3,1/3] with radius 1/3. Copy the following code to a file on your MATLAB® path named circlecon.m.

% Copyright 2015 The MathWorks, Inc.

function [c,ceq] = circlecon(x)
c = (x(1)-1/3)^2 + (x(2)-1/3)^2 - (1/3)^2;
ceq = [];


There are no linear constraints, so set those arguments to [].
A = [];
b = [];
Aeq = [];
beq = [];

Choose an initial point satisfying all the constraints.
x0 = [1/4,1/4];

Solve the problem.
nonlcon = @circlecon;
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.




x =

    0.5000    0.2500


Nondefault Options



Set options to view iterations as they occur and to use a different algorithm.



To observe the fmincon solution process, set the Display option to 'iter'. Also, try the 'sqp' algorithm, which is sometimes faster or more accurate than the default 'interior-point' algorithm.
options = optimoptions('fmincon','Display','iter','Algorithm','sqp');

Find the minimum of Rosenbrock's function on the unit disk, 
$||x||^2 \le 1$. First create a function that represents the nonlinear constraint. Save this as a file named unitdisk.m on your MATLAB® path.

% Copyright 2015 The MathWorks, Inc.

function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [];


Create the remaining problem specifications. Then run fmincon.
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
nonlcon = @unitdisk;
x0 = [0,0];
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

                                                          Norm of First-order
 Iter F-count            f(x) Feasibility  Steplength        step  optimality
    0       3    1.000000e+00   0.000e+00                           2.000e+00
    1      12    8.913011e-01   0.000e+00   1.176e-01   2.353e-01   1.107e+01
    2      22    8.047847e-01   0.000e+00   8.235e-02   1.900e-01   1.330e+01
    3      28    4.197517e-01   0.000e+00   3.430e-01   1.217e-01   6.153e+00
    4      31    2.733703e-01   0.000e+00   1.000e+00   5.254e-02   4.587e-01
    5      34    2.397111e-01   0.000e+00   1.000e+00   7.498e-02   3.029e+00
    6      37    2.036002e-01   0.000e+00   1.000e+00   5.960e-02   3.019e+00
    7      40    1.164353e-01   0.000e+00   1.000e+00   1.459e-01   1.058e+00
    8      43    1.161753e-01   0.000e+00   1.000e+00   1.754e-01   7.383e+00
    9      46    5.901601e-02   0.000e+00   1.000e+00   1.547e-02   7.278e-01
   10      49    4.533081e-02   2.898e-03   1.000e+00   5.393e-02   1.252e-01
   11      52    4.567454e-02   2.225e-06   1.000e+00   1.492e-03   1.679e-03
   12      55    4.567481e-02   4.406e-12   1.000e+00   2.095e-06   1.501e-05
   13      58    4.567481e-02   0.000e+00   1.000e+00   2.160e-09   1.511e-05

Local minimum possible. Constraints satisfied.

fmincon stopped because the size of the current step is less than
the default value of the step size tolerance and constraints are 
satisfied to within the default value of the constraint tolerance.




x =

    0.7864    0.6177


Include Gradient



Include gradient evaluation in the objective function for faster or more reliable computations.



Include the gradient evaluation as a conditionalized output in the objective function file. For details, see Including Derivatives. The objective function is Rosenbrock's function,

$$ f(x) = 100{\left( {{x_2} - x_1^2} \right)^2} +&#xA;{(1 - {x_1})^2},$$
which has gradient

$$\nabla f(x) = \left[ {\begin{array}{*{20}{c}}&#xA;{ - 400\left( {{x_2} - x_1^2} \right){x_1} - 2\left( {1 - {x_1}} \right)}\\&#xA;{200\left( {{x_2} - x_1^2} \right)}&#xA;\end{array}} \right].$$

% Copyright 2015 The MathWorks, Inc.

function [f,g] = rosenbrockwithgrad(x)
% Calculate objective f
f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;

if nargout > 1 % gradient required
    g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1));
        200*(x(2)-x(1)^2)];
end


Save this code as a file named rosenbrockwithgrad.m on your MATLAB® path.
Create options to use the objective function gradient.
options = optimoptions('fmincon','GradObj','on');

Create the other inputs for the problem. Then call fmincon.
fun = @rosenbrockwithgrad;
x0 = [-1,2];
A = [];
b = [];
Aeq = [];
beq = [];
lb = [-2,-2];
ub = [2,2];
nonlcon = [];
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.




x =

    1.0000    1.0000


Use a Problem Structure


Solve the same problem as in Nondefault Options using a problem
structure instead of separate arguments.


Create
the options and a problem structure. See problem for the field names and required
fields.
options = optimoptions('fmincon','Display','iter','Algorithm','sqp');
problem.options = options;
problem.solver = 'fmincon';
problem.objective = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
problem.x0 = [0,0];
Create a function file for the nonlinear constraint function
representing norm(x)2 ≤ 1.
function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [ ];
Save this as a file named unitdisk.m on your MATLAB® path.
Include the nonlinear constraint function in problem.
problem.nonlcon = @unitdisk;
Solve the problem.
x = fmincon(problem)
                                                          Norm of First-order
 Iter F-count            f(x) Feasibility  Steplength        step  optimality
    0       3    1.000000e+00   0.000e+00                           2.000e+00
    1      12    8.913011e-01   0.000e+00   1.176e-01   2.353e-01   1.107e+01
    2      22    8.047847e-01   0.000e+00   8.235e-02   1.900e-01   1.330e+01
    3      28    4.197517e-01   0.000e+00   3.430e-01   1.217e-01   6.153e+00
    4      31    2.733703e-01   0.000e+00   1.000e+00   5.254e-02   4.587e-01
    5      34    2.397111e-01   0.000e+00   1.000e+00   7.498e-02   3.029e+00
    6      37    2.036002e-01   0.000e+00   1.000e+00   5.960e-02   3.019e+00
    7      40    1.164353e-01   0.000e+00   1.000e+00   1.459e-01   1.058e+00
    8      43    1.161753e-01   0.000e+00   1.000e+00   1.754e-01   7.383e+00
    9      46    5.901601e-02   0.000e+00   1.000e+00   1.547e-02   7.278e-01
   10      49    4.533081e-02   2.898e-03   1.000e+00   5.393e-02   1.252e-01
   11      52    4.567454e-02   2.225e-06   1.000e+00   1.492e-03   1.679e-03
   12      55    4.567481e-02   4.406e-12   1.000e+00   2.095e-06   1.501e-05
   13      58    4.567481e-02   0.000e+00   1.000e+00   2.160e-09   1.511e-05

Local minimum possible. Constraints satisfied.

fmincon stopped because the size of the current step is less than
the default value of the step size tolerance and constraints are 
satisfied to within the default value of the constraint tolerance.

<stopping criteria details>
x =

    0.7864    0.6177
The iterative display and solution are the same as in Nondefault Options.
Obtain the Objective Function Value


Call fmincon with the fval output
to obtain the value of the objective function at the solution.


The Bound Constraints example shows two solutions.
Which is better? Run the example requesting the fval output
as well as the solution.
fun = @(x)1+x(1)./(1+x(2)) - 3*x(1).*x(2) + x(2).*(1+x(1));
lb = [0,0];
ub = [1,2];
A = [];
b = [];
Aeq = [];
beq = [];
x0 = [0.5,1];
[x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.

<stopping criteria details>
x =

    1.0000    2.0000


fval =

   -0.6667
Run the problem using a different starting point x0.
x0 = x0/5;
[x2,fval2] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.

<stopping criteria details>
x2 =

   1.0e-06 *

    0.4000    0.4000


fval2 =

    1.0000
This solution has an objective function value fval2
= 1, which is higher than the first value fval
= -0.6667. The first solution x has a
lower local minimum objective function value.
Examine Solution Using Extra Outputs



To easily examine the quality of a solution, request the exitflag and output outputs.



Set up the problem of minimizing Rosenbrock's function on the unit disk, 
$||x||^2 \le 1$. First create a function that represents the nonlinear constraint. Save this as a file named unitdisk.m on your MATLAB® path.

% Copyright 2015 The MathWorks, Inc.

function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [];


Create the remaining problem specifications.
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
nonlcon = @unitdisk;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
x0 = [0,0];

Call fmincon using the fval, exitflag, and output outputs.
[x,fval,exitflag,output] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.




x =

    0.7864    0.6177


fval =

    0.0457


exitflag =

     1


output = 

         iterations: 24
          funcCount: 84
    constrviolation: 0
           stepsize: 6.9162e-06
          algorithm: 'interior-point'
      firstorderopt: 2.4373e-08
       cgiterations: 4
            message: 'Local minimum found that satisfies the constraints....'


  • The exitflag value 1 indicates that the solution is a local minimum.
  • The output structure reports several statistics about the solution process. In particular, it gives the number of iterations in output.iterations, number of function evaluations in output.funcCount, and the feasibility in output.constrviolation.
Obtain All Outputs


fmincon optionally returns
several outputs that you can use for analyzing the reported solution.


Set up the problem of minimizing Rosenbrock's function
on the unit disk. First create a function that represents the nonlinear
constraint. Save this as a file named unitdisk.m on
your MATLAB path.
function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [];
Create the remaining problem specifications.
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
nonlcon = @unitdisk;
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];
x0 = [0,0];
Request all fmincon outputs.
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.

<stopping criteria details>


x =

    0.7864    0.6177


fval =

    0.0457


exitflag =

     1


output = 

         iterations: 24
          funcCount: 84
    constrviolation: 0
           stepsize: 6.9160e-06
          algorithm: 'interior-point'
      firstorderopt: 2.0624e-08
       cgiterations: 4
            message: 'Local minimum found that satisfies the constraints.

Optimizati...'


lambda = 

         eqlin: [0x1 double]
      eqnonlin: [0x1 double]
       ineqlin: [0x1 double]
         lower: [2x1 double]
         upper: [2x1 double]
    ineqnonlin: 0.1215


grad =

   -0.1911
   -0.1501


hessian =

  497.2871 -314.5574
 -314.5574  200.2378
  • The lambda.ineqnonlin output shows
that the nonlinear constraint is active at the solution, and gives
the value of the associated Lagrange multiplier.
  • The grad output gives the value
of the gradient of the objective function at the solution x.
  • The hessian output is described
in fmincon Hessian.
Related Examples
Input Arguments
collapse all
fun — Function to minimizefunction handle | function name


Function to minimize, specified as a function handle or function
name. fun is a function that accepts a vector or
array x and returns a real scalar f,
the objective function evaluated at x.


Specify fun as a function handle for a file:


x = fmincon(@myfun,x0,A,b)


where myfun is a MATLAB function such
as


function f = myfun(x)
f = ...            % Compute function value at x


You can also specify fun as a function handle
for an anonymous function:


x = fmincon(@(x)norm(x)^2,x0,A,b);


If you can compute the gradient of fun and the GradObj option
is set to 'on', as set by
options = optimoptions('fmincon','GradObj','on')
then fun must
return the gradient vector g(x) in the second output
argument.


If you can also compute the Hessian matrix and the Hessian option
is set to 'on' via options = optimoptions('fmincon','Hessian','user-supplied') and the Algorithm option
is trust-region-reflective, fun must
return the Hessian value H(x), a symmetric matrix,
in a third output argument. fun can give a sparse
Hessian. See Writing Objective Functions for
details.


If you can also compute the Hessian matrix and the Algorithm option
is set to 'interior-point', there are several ways
to pass the Hessian to fmincon. For more information,
see Hessian. For an example using Symbolic Math Toolbox™ to
compute the gradient and Hessian, see Symbolic Math Toolbox Calculates Gradients and Hessians.


The interior-point and trust-region-reflective algorithms
allow you to supply a Hessian multiply function. This function gives
the result of a Hessian-times-vector product without computing the
Hessian directly. This can save memory. See Hessian Multiply Function.


Example: fun = @(x)sin(x(1))*cos(x(2))


Data Types: char | function_handle
x0 — Initial pointreal vector | real array


Initial point, specified as a real vector or real array. Solvers
use the number of elements in, and size of, x0 to
determine the number and size of variables that fun accepts.


Example: x0 = [1,2,3,4]


Data Types: double
A — Linear inequality constraintsreal matrix


Linear inequality constraints, specified as a real matrix. A is
an M-by-N matrix, where M is
the number of inequalities, and N is the number
of variables (number of elements in x0). For
large problems, pass A as a sparse matrix.


A encodes the M linear
inequalities


A*x <= b,


where x is the column vector of N variables x(:),
and b is a column vector with M elements.


For example, to specify


x1 + 2x2 ≤
10
3x1 +
4x2 ≤ 20
5x1 +
6x2 ≤ 30,


give these constraints:


A = [1,2;3,4;5,6];
b = [10;20;30];


Example: To specify that the x-components add up to 1 or less,
take A = ones(1,N) and b = 1


Data Types: double
b — Linear inequality constraintsreal vector


Linear inequality constraints, specified as a real vector. b is
an M-element vector related to the A matrix.
If you pass b as a row vector, solvers internally
convert b to the column vector b(:).
For large problems, pass b as a sparse vector.


b encodes the M linear
inequalities


A*x <= b,


where x is the column vector of N variables x(:),
and A is a matrix of size M-by-N.


For example, to specify


x1 + 2x2 ≤
10
3x1 +
4x2 ≤ 20
5x1 +
6x2 ≤ 30,


give these constraints:


A = [1,2;3,4;5,6];
b = [10;20;30];


Example: To specify that the x-components sum to 1 or less, take A
= ones(1,N) and b = 1


Data Types: double
Aeq — Linear equality constraintsreal matrix


Linear equality constraints, specified as a real matrix. Aeq is
an Me-by-N matrix, where Me is
the number of equalities, and N is the number of
variables (number of elements in x0). For large
problems, pass Aeq as a sparse matrix.


Aeq encodes the Me linear
equalities


Aeq*x = beq,


where x is the column vector of N variables x(:),
and beq is a column vector with Me elements.


For example, to specify


x1 + 2x2 +
3x3 = 10
2x1 +
4x2 + x3 =
20,


give these constraints:


Aeq = [1,2,3;2,4,1];
beq = [10;20];


Example: To specify that the x-components sum to 1, take Aeq
= ones(1,N) and beq = 1


Data Types: double
beq — Linear equality constraintsreal vector


Linear equality constraints, specified as a real vector. beq is
an Me-element vector related to the Aeq matrix.
If you pass beq as a row vector, solvers internally
convert beq to the column vector beq(:).
For large problems, pass beq as a sparse vector.


beq encodes the Me linear
equalities


Aeq*x = beq,


where x is the column vector of N variables x(:),
and Aeq is a matrix of size Meq-by-N.


For example, to specify


x1 + 2x2 +
3x3 = 10
2x1 +
4x2 + x3 =
20,


give these constraints:


Aeq = [1,2,3;2,4,1];
beq = [10;20];


Example: To specify that the x-components sum to 1, take Aeq
= ones(1,N) and beq = 1


Data Types: double
lb — Lower boundsreal vector | real array


Lower bounds, specified as a real vector or real array. If the
number of elements in x0 is equal to that of lb,
then lb specifies that


x(i) >= lb(i) for all i.


If numel(lb) < numel(x0), then lb specifies
that


x(i) >= lb(i) for 1 <=
i <= numel(lb).


In this case, solvers issue a warning.


Example: To specify that all x-components are positive, lb
= zeros(size(x0))
Data Types: double
ub — Upper boundsreal vector | real array


Upper bounds, specified as a real vector or real array. If the
number of elements in x0 is equal to that of ub,
then ub specifies that


x(i) <= ub(i) for all i.


If numel(ub) < numel(x0), then ub specifies
that


x(i) <= ub(i) for 1 <=
i <= numel(ub).


In this case, solvers issue a warning.


Example: To specify that all x-components are less than one, ub
= ones(size(x0))
Data Types: double
nonlcon — Nonlinear constraintsfunction handle | function name


Nonlinear constraints, specified as a function handle or function
name. nonlcon is a function that accepts a vector
or array x and returns two arrays, c(x) and ceq(x).


  • c(x) is the array of nonlinear
inequality constraints at x. fmincon attempts
to satisfy
    c(x) <= 0 for all entries of c.
  • ceq(x) is the array of nonlinear
equality constraints at x. fmincon attempts
to satisfy
    ceq(x) = 0 for all entries of ceq.


For example,


x = fmincon(@myfun,x0,A,b,Aeq,beq,lb,ub,@mycon)


where mycon is a MATLAB function such
as
function [c,ceq] = mycon(x)
c = ...     % Compute nonlinear inequalities at x.
ceq = ...   % Compute nonlinear equalities at x.
If
the gradients of the constraints can also be computed and the GradConstr option
is 'on', as set by
options = optimoptions('fmincon','GradConstr','on')
then nonlcon must
also return, in the third and fourth output arguments, GC,
the gradient of c(x), and GCeq,
the gradient of ceq(x). GC and GCeq can
be sparse or dense. If GC or GCeq is
large, with relatively few nonzero entries, save running time and
memory in the interior-point algorithm by representing
them as sparse matrices. For more information, see Nonlinear Constraints.


Data Types: char | function_handle
options — Optimization optionsoutput of optimoptions | structure such as optimset returns


Optimization options, specified as the output of optimoptions or
a structure such as optimset returns.


Some options apply to all algorithms, and others are relevant
for particular algorithms. See Optimization Options Reference for detailed information.


All Algorithms


Algorithm
Choose the optimization algorithm:
  • 'interior-point' (default)
  • 'trust-region-reflective'
  • 'sqp'
  • 'active-set'
For information on choosing the algorithm, see Choosing the Algorithm.
The trust-region-reflective algorithm
requires:
  • A gradient to be supplied in the objective function
  • GradObj to be set to 'on'
  • Either bound constraints or linear equality constraints,
but not both
 If you select the 'trust-region-reflective' algorithm
and these conditions are not all satisfied, fmincon throws
an error.
The 'active-set' and 'sqp' algorithms
are not large-scale. See Large-Scale vs. Medium-Scale Algorithms.


DerivativeCheck
Compare user-supplied derivatives
(gradients of objective or constraints) to finite-differencing derivatives.
Choices are 'off' (default) or 'on'.


Diagnostics
Display diagnostic information
about the function to be minimized or solved. Choices are 'off' (default)
or 'on'.


DiffMaxChange
Maximum change in variables for
finite-difference gradients (a positive scalar). The default is Inf.


DiffMinChange
Minimum change in variables for
finite-difference gradients (a positive scalar). The default is 0.


Display
Level of display (see Iterative Display):
  • 'off' or 'none' displays
no output.
  • 'iter' displays output at each
iteration, and gives the default exit message.
  • 'iter-detailed' displays output
at each iteration, and gives the technical exit message.
  • 'notify' displays output only if
the function does not converge, and gives the default exit message.
  • 'notify-detailed' displays output
only if the function does not converge, and gives the technical exit
message.
  • 'final' (default) displays only
the final output, and gives the default exit message.
  • 'final-detailed' displays only
the final output, and gives the technical exit message.


FinDiffRelStep
Scalar or vector step size factor for finite differences. When
you set FinDiffRelStep to a vector v,
forward finite differences steps delta are
delta
= v.*sign′(x).*max(abs(x),TypicalX);
where sign′(x)
= sign(x) except sign′(0) = 1.
Central finite differences are
delta = v.*max(abs(x),TypicalX);
Scalar FinDiffRelStep expands
to a vector. The default is sqrt(eps) for forward
finite differences, and eps^(1/3) for central finite
differences.


FinDiffType
Finite differences, used to estimate
gradients, are either 'forward' (default), or 'central' (centered). 'central' takes
twice as many function evaluations but should be more accurate. The
trust-region-reflective algorithm uses FinDiffType only
when DerivativeCheck is set to 'on'.
fmincon is
careful to obey bounds when estimating both types of finite differences.
So, for example, it could take a backward, rather than a forward,
difference to avoid evaluating at a point outside bounds. However,
for the interior-point algorithm, 'central' differences
might violate bounds during their evaluation if the AlwaysHonorConstraints option
is set to 'none'.


FunValCheck
Check whether objective function
values are valid. The default setting, 'off', does
not perform a check. The 'on' setting displays
an error when the objective function returns a value that is complex, Inf,
or NaN.


GradConstr
Gradient for nonlinear constraint
functions defined by the user. When set to the default, 'off', fmincon estimates
gradients of the nonlinear constraints by finite differences. When
set to 'on', fmincon expects
the constraint function to have four outputs, as described in nonlcon. The trust-region-reflective algorithm
does not accept nonlinear constraints.


GradObj
Gradient for the objective function
defined by the user. See the description of fun to see how to define the gradient in fun.
The default, 'off', causes fmincon to
estimate gradients using finite differences. Set to 'on' to
have fmincon use a user-defined gradient of the
objective function. You must provide the gradient, and set GradObj to 'on',
to use the trust-region-reflective method. 


MaxFunEvals
Maximum number of function evaluations
allowed, a positive integer. The default value for all algorithms
except interior-point is 100*numberOfVariables;
for the interior-point algorithm the default is 3000.
See Tolerances and Stopping Criteria and Iterations and Function Counts.


MaxIter
Maximum number of iterations allowed,
a positive integer. The default value for all algorithms except interior-point is 400;
for the interior-point algorithm the default is 1000.
See Tolerances and Stopping Criteria and Iterations and Function Counts.


OutputFcn
Specify one or more user-defined
functions that an optimization function calls at each iteration, either
as a function handle or as a cell array of function handles. The default
is none ([]). See Output Function.


PlotFcns
Plot various measures of progress
while the algorithm executes, select from predefined plots or write
your own. Pass a function handle or a cell array of function handles.
The default is none ([]).  
  • @optimplotx plots the current point
  • @optimplotfunccount plots the function
count
  • @optimplotfval plots the function
value
  • @optimplotconstrviolation plots
the maximum constraint violation
  • @optimplotstepsize plots the step
size
  • @optimplotfirstorderopt plots the
first-order optimality measure
For information on writing a custom plot function,
see Plot Functions.


TolCon
Tolerance on the constraint violation,
a positive scalar. The default is 1e-6. See Tolerances and Stopping Criteria.


TolFun
Termination tolerance on the function
value, a positive scalar. The default is 1e-6.
See Tolerances and Stopping Criteria.


TolX
Termination tolerance on x,
a positive scalar. The default value for all algorithms except 'interior-point' is 1e-6;
for the 'interior-point' algorithm, the default
is 1e-10. See Tolerances and Stopping Criteria.


TypicalX
Typical x values.
The number of elements in TypicalX is equal to
the number of elements in x0, the starting point.
The default value is ones(numberofvariables,1). fmincon uses TypicalX for
scaling finite differences for gradient estimation.
The 'trust-region-reflective' algorithm
uses TypicalX only for the DerivativeCheck option.


UseParallel
When true, fmincon estimates
gradients in parallel. Disable by setting to the default, false. trust-region-reflective requires
a gradient in the objective, so UseParallel does
not apply. See Parallel Computing.


Trust-Region-Reflective Algorithm


Hessian
If 'off' (default), fmincon approximates
the Hessian using finite differences. If 'on' or 'user-supplied', fmincon uses
a user-defined Hessian (defined in fun), or Hessian information (when using HessMult),
for the objective function. See Hessian.


HessMult
Function handle for Hessian multiply function.
For large-scale structured problems, this function computes the Hessian
matrix product H*Y without actually forming H.
The function is of the form
W = hmfun(Hinfo,Y)
where Hinfo contains
a matrix used to compute H*Y. 
The
first argument is the same as the third argument returned by the objective
function fun, for example
[f,g,Hinfo] = fun(x)
Y is
a matrix that has the same number of rows as there are dimensions
in the problem. The matrix W = H*Y, although H is
not formed explicitly. fmincon uses Hinfo to
compute the preconditioner. For information on how to supply values
for any additional parameters hmfun needs, see Passing Extra Parameters.
    Note  


Hessian must be set to 'on' or 'user-supplied' for fmincon to
pass Hinfo from fun to hmfun.
See Hessian Multiply Function. See Minimization with Dense Structured Hessian, Linear Equalities for
an example.


 


HessPattern
Sparsity pattern of the Hessian
for finite differencing. Set HessPattern(i,j) = 1 when
you can have ∂2fun/∂x(i)∂x(j) ≠ 0. Otherwise, set HessPattern(i,j)
= 0.
Use HessPattern when
it is inconvenient to compute the Hessian matrix H in fun,
but you can determine (say, by inspection) when the ith
component of the gradient of fun depends on x(j). fmincon can
approximate H via sparse finite differences (of
the gradient) if you provide the sparsity structure of H as
the value for HessPattern. In other words, provide
the locations of the nonzeros.
When the structure is unknown,
do not set HessPattern. The default behavior is
as if HessPattern is a dense matrix of ones. Then fmincon computes
a full finite-difference approximation in each iteration. This computation
can be very expensive for large problems, so it is usually better
to determine the sparsity structure.
 


MaxPCGIter
Maximum number of preconditioned
conjugate gradient (PCG) iterations, a positive scalar. The default
is max(1,floor(numberOfVariables/2)). For more
information, see Preconditioned Conjugate Gradient Method.
 


PrecondBandWidth
Upper bandwidth of preconditioner
for PCG, a nonnegative integer. By default, diagonal preconditioning
is used (upper bandwidth of 0). For some problems, increasing the
bandwidth reduces the number of PCG iterations. Setting PrecondBandWidth to Inf uses
a direct factorization (Cholesky) rather than the conjugate gradients
(CG). The direct factorization is computationally more expensive than
CG, but produces a better quality step towards the solution.
 


TolPCG
Termination tolerance on the PCG
iteration, a positive scalar. The default is 0.1.
 


Active-Set Algorithm 


MaxSQPIter
Maximum number of SQP iterations
allowed, a positive integer. The default is 10*max(numberOfVariables,
numberOfInequalities + numberOfBounds).
 


RelLineSrchBnd
Relative bound (a real nonnegative
scalar value) on the line search step length. The total displacement
in x satisfies |Δx(i)| ≤ relLineSrchBnd· max(|x(i)|,|typicalx(i)|).
This option provides control over the magnitude of the displacements
in x for cases in which the solver takes steps
that are considered too large. The default is no bounds ([]).
 


RelLineSrchBndDuration
Number of iterations for which
the bound specified in RelLineSrchBnd should be
active (default is 1).
 


TolConSQP
Termination tolerance on inner
iteration SQP constraint violation, a positive scalar. The default
is 1e-6.
 


Interior-Point Algorithm 


AlwaysHonorConstraints
The default 'bounds' ensures
that bound constraints are satisfied at every iteration. Disable by
setting to 'none'.
 


HessFcn
Function handle to a user-supplied
Hessian (see Hessian). This is
used when the Hessian option is set to 'user-supplied'.
 


Hessian
Chooses how fmincon calculates
the Hessian (see Hessian). The
choices are:
  • 'bfgs' (default)
  • 'fin-diff-grads'
  • 'lbfgs'
  • {'lbfgs',Positive Integer}
  • 'user-supplied'
 


HessMult
Handle to a user-supplied function
that gives a Hessian-times-vector product (see Hessian Multiply Function). This is used when the Hessian option
is set to 'user-supplied'.
 


InitBarrierParam
Initial barrier value, a positive
scalar. Sometimes it might help to try a value above the default 0.1,
especially if the objective or constraint functions are large.
 


InitTrustRegionRadius
Initial radius of the trust region,
a positive scalar. On badly scaled problems it might help to choose
a value smaller than the default n,
where n is the number of variables.
 


MaxProjCGIter
A tolerance (stopping criterion)
for the number of projected conjugate gradient iterations; this is
an inner iteration, not the number of iterations of the algorithm.
This positive integer has a default value of 2*(numberOfVariables - numberOfEqualities).
 


ObjectiveLimit
A tolerance (stopping criterion)
that is a scalar. If the objective function value goes below ObjectiveLimit and
the iterate is feasible, the iterations halt, because the problem
is presumably unbounded. The default value is -1e20.
 


ScaleProblem
'obj-and-constr' causes
the algorithm to normalize all constraints and the objective function.
Disable by setting to the default 'none'.
 


SubproblemAlgorithm
Determines how the iteration step
is calculated. The default, 'ldl-factorization',
is usually faster than 'cg' (conjugate gradient),
though 'cg' might be faster for large problems
with dense Hessians. 
 


TolProjCG
A relative tolerance (stopping
criterion) for projected conjugate gradient algorithm; this is for
an inner iteration, not the algorithm iteration. This positive scalar
has a default of 0.01.
 


TolProjCGAbs
Absolute tolerance (stopping criterion)
for projected conjugate gradient algorithm; this is for an inner iteration,
not the algorithm iteration. This positive scalar has a default of 1e-10.
 


SQP Algorithm 


ObjectiveLimit
A tolerance (stopping criterion)
that is a scalar. If the objective function value goes below ObjectiveLimit and
the iterate is feasible, the iterations halt, because the problem
is presumably unbounded. The default value is -1e20.
 


ScaleProblem
'obj-and-constr' causes
the algorithm to normalize all constraints and the objective function.
Disable by setting to the default 'none'.
 




Example: options = optimoptions('fmincon','GradObj','on','GradConstr','on')


problem — Problem structurestructure


Problem structure, specified as a structure with the following
fields:


Field NameEntry


objective 
Objective function


x0 
Initial point for x


Aineq 
Matrix for linear inequality constraints


bineq 
Vector for linear inequality constraints


Aeq 
Matrix for linear equality constraints


beq 
Vector for linear equality constraints


lbVector of lower bounds


ubVector of upper bounds


nonlcon 
Nonlinear constraint function


solver 
'fmincon'


options 
Options created with optimoptions




You must supply at least the objective, x0, solver,
and options fields in the problem structure.


The simplest way to obtain a problem structure
is to export the problem from the Optimization app.


Data Types: struct
Output Arguments
collapse all
x — Solutionreal vector | real array


Solution, returned as a real vector or real array. The size
of x is the same as the size of x0.
Typically, x is a local solution to the problem
when exitflag is positive. For information on
the quality of the solution, see When the Solver Succeeds.


fval — Objective function value at solutionreal number


Objective function value at the solution, returned as a real
number. Generally, fval = fun(x). 


exitflag — Reason fmincon stoppedinteger


Reason fmincon stopped, returned as an
integer.


All Algorithms:


1
First-order optimality measure was less than options.TolFun,
and maximum constraint violation was less than options.TolCon.


0
Number of iterations exceeded options.MaxIter or
number of function evaluations exceeded options.MaxFunEvals.


-1
Stopped by an output function or plot function.


-2
No feasible point was found.


trust-region-reflective, interior-point,
and sqp algorithms:


2
Change in x was less than options.TolX and
maximum constraint violation was less than options.TolCon.


trust-region-reflective algorithm
only:


3
Change in the objective function value was less than options.TolFun and
maximum constraint violation was less than options.TolCon.


active-set algorithm
only:


4
Magnitude of the search direction was less than 2*options.TolX and
maximum constraint violation was less than options.TolCon.


5
Magnitude of directional derivative in search direction
was less than 2*options.TolFun and maximum constraint
violation was less than options.TolCon.


interior-point and sqp algorithms:


-3
Objective function at current iteration went below options.ObjectiveLimit and
maximum constraint violation was less than options.TolCon.




output — Information about the optimization processstructure


Information about the optimization process, returned as a structure
with fields:


iterations
Number of iterations taken


funcCount
Number of function evaluations


lssteplength
Size of line search step relative to search direction
(active-set and sqp algorithms
only)


constrviolation
Maximum of constraint functions


stepsize
Length of last displacement in x (not
in active-set algorithm)


algorithm
Optimization algorithm used


cgiterations
Total number of PCG iterations (trust-region-reflective and interior-point algorithms)


firstorderopt
Measure of first-order optimality 


message
Exit message




lambda — Lagrange multipliers at the solutionstructure


Lagrange multipliers at the solution, returned as a structure
with fields:


lower
Lower bounds corresponding to lb


upper
Upper bounds corresponding to ub


ineqlin
Linear inequalities corresponding to A and b


eqlin
Linear equalities corresponding to Aeq and beq


ineqnonlin
Nonlinear inequalities corresponding to the c in nonlcon


eqnonlin
Nonlinear equalities corresponding to the ceq in nonlcon




grad — Gradient at the solutionreal vector


Gradient at the solution, returned as a real vector. grad gives
the gradient of fun at the point x(:).


hessian — Approximate Hessianreal matrix


Approximate Hessian, returned as a real matrix. For the meaning
of hessian, see Hessian.


Limitations
  • fmincon is a gradient-based method
that is designed to work on problems where the objective and constraint
functions are both continuous and have continuous first derivatives.
  • For the 'trust-region-reflective' algorithm,
you must provide the gradient in fun.
  • The 'trust-region-reflective' algorithm
does not allow equal upper and lower bounds. For example, if lb(2)==ub(2), fmincon gives
this error:
    Equal upper and lower bounds not permitted in trust-region-reflective algorithm. Use
either interior-point or SQP algorithms instead.
  • There are two different syntaxes for passing a Hessian,
and there are two different syntaxes for passing a HessMult function;
one for trust-region-reflective, and another for interior-point.
See Hessian.
    • For trust-region-reflective, the
Hessian of the Lagrangian is the same as the Hessian of the objective
function. You pass that Hessian as the third output of the objective
function. 
    • For interior-point, the Hessian
of the Lagrangian involves the Lagrange multipliers and the Hessians
of the nonlinear constraint functions. You pass the Hessian as a separate
function that takes into account both the position x and
the Lagrange multiplier structure lambda.
  • When the problem is infeasible, fmincon attempts
to minimize the maximum constraint value.
More About
expand all
Hessian
fmincon uses a Hessian
as an optional input. This Hessian is the matrix of second derivatives
of the Lagrangian (see Equation 3-1), namely,
∇xx2L(x,λ)=∇2f(x)+∑λi∇2ci(x)+∑λi∇2ceqi(x).(14-1)
The various fmincon algorithms handle input
Hessians differently:
  • The active-set and sqp algorithms
do not accept a user-supplied Hessian. They compute a quasi-Newton
approximation to the Hessian of the Lagrangian.
  • The trust-region-reflective algorithm
can accept a user-supplied Hessian as the final output of the objective
function. Since this algorithm has only bounds or linear constraints,
the Hessian of the Lagrangian is same as the Hessian of the objective
function. See Writing Scalar Objective Functions for
details on how to pass the Hessian to fmincon.
Indicate that you are supplying a Hessian by
    options = optimoptions('fmincon','Algorithm','trust-region-reflective','Hessian','user-supplied');
    If
you do not pass a Hessian, the algorithm computes a finite-difference
approximation.
  • The interior-point algorithm
can accept a user-supplied Hessian as a separately defined function—it
is not computed in the objective function. The syntax is
    hessian = hessianfcn(x, lambda)
    hessian is
an n-by-n matrix, sparse or
dense, where n is the number of variables. If hessian is
large and has relatively few nonzero entries, save running time and
memory by representing hessian as a sparse matrix. lambda is
a structure with the Lagrange multiplier vectors associated with the
nonlinear constraints:
    lambda.ineqnonlin
lambda.eqnonlin
    fmincon computes
the structure lambda. hessianfcn must
calculate the sums in Equation 14-1. Indicate that you are supplying
a Hessian by
    options = optimoptions('fmincon','Algorithm','interior-point',...
    'Hessian','user-supplied','HessFcn',@hessianfcn);
    For an example, see fmincon Interior-Point Algorithm with Analytic Hessian. 
The interior-point algorithm has
several more options for Hessians; see Choose Input Hessian for interior-point fmincon:
  • options = optimoptions('fmincon','Hessian','bfgs');
    fmincon calculates the Hessian by a dense
quasi-Newton approximation. This is the default Hessian approximation.
  • options = optimoptions('fmincon','Hessian','lbfgs');
    fmincon calculates the Hessian by a limited-memory,
large-scale quasi-Newton approximation. The default memory, 10 iterations,
is used.
  • options = optimoptions('fmincon','Hessian',{'lbfgs',positive integer});
    fmincon calculates the Hessian by a limited-memory,
large-scale quasi-Newton approximation. The positive integer specifies
how many past iterations should be remembered.
  • options = optimoptions('fmincon','Hessian','fin-diff-grads',... 
     'SubproblemAlgorithm','cg','GradObj','on',... 
    
'GradConstr','on');
    fmincon calculates a Hessian-times-vector
product by finite differences of the gradient(s). You must supply
the gradient of the objective function, and also gradients of nonlinear
constraints (if they exist).
Hessian Multiply Function
The interior-point and trust-region-reflective algorithms
allow you to supply a Hessian multiply function. This function gives
the result of a Hessian-times-vector product, without computing the
Hessian directly. This can save memory.
The syntaxes for the two algorithms differ:
  • For the interior-point algorithm,
the syntax is
    W = HessMultFcn(x,lambda,v);
    The result W should be the product H*v,
where H is the Hessian of the Lagrangian at x (see Equation 14-1), lambda is
the Lagrange multiplier (computed by fmincon),
and v is a vector of size n-by-1.
Set options as follows:
    options = optimoptions('fmincon','Algorithm','interior-point','Hessian','user-supplied',... 
    'SubproblemAlgorithm','cg','HessMult',@HessMultFcn);
    Supply the function HessMultFcn, which returns
an n-by-1 vector, where n is
the number of dimensions of x. The HessMult option
enables you to pass the result of multiplying the Hessian by a vector
without calculating the Hessian.
  • The trust-region-reflective algorithm
does not involve lambda:
    W = HessMultFcn(H,v);
    The result W = H*v. fmincon passes H as
the value returned in the third output of the objective function (see Writing Scalar Objective Functions). fmincon also
passes v, a vector or matrix with n rows.
The number of columns in v can vary, so write HessMultFcn to
accept an arbitrary number of columns. H does not
have to be the Hessian; rather, it can be anything that enables you
to calculate W = H*v.
    Set options as follows:
    options = optimoptions('fmincon','Algorithm','trust-region-reflective',... 
    'Hessian','user-supplied','HessMult',@HessMultFcn);
    For an example using a Hessian multiply function with the trust-region-reflective algorithm,
see Minimization with Dense Structured Hessian, Linear Equalities.
Algorithms
Interior-Point Optimization
This algorithm is described in fmincon Interior Point Algorithm. There is more extensive
description in [1], [41], and [9].
SQP Optimization
The fmincon 'sqp' algorithm
is similar to the 'active-set' algorithm described
in Active-Set Optimization. fmincon SQP Algorithm describes the main
differences. In summary, these differences are:
Active-Set Optimization
fmincon uses a sequential quadratic programming (SQP) method. In this
method, the function solves a quadratic
programming (QP) subproblem at each iteration. fmincon updates
an estimate of the Hessian of the Lagrangian at each iteration using
the BFGS formula (see fminunc and
references [7] and [8]).
fmincon performs a line search using a
merit function similar to that proposed by [6], [7], and [8]. The QP subproblem is solved using
an active set strategy similar to that described in [5]. fmincon Active Set Algorithm describes this algorithm in
detail. 
See also SQP Implementation for
more details on the algorithm used.
Trust-Region-Reflective Optimization
The 'trust-region-reflective' algorithm is
a subspace trust-region method and is based on the interior-reflective
Newton method described in [3] and [4]. Each iteration involves the approximate
solution of a large linear system using the method of preconditioned
conjugate gradients (PCG). See the trust-region and preconditioned
conjugate gradient method descriptions in fmincon Trust Region Reflective Algorithm.
References
[1] Byrd, R. H., J. C. Gilbert, and J. Nocedal.
"A Trust Region Method Based on Interior Point Techniques for
Nonlinear  Programming." Mathematical Programming,
Vol 89, No. 1, 2000, pp. 149–185.
[2] Byrd, R. H., Mary E. Hribar, and Jorge Nocedal.
"An Interior Point Algorithm for Large-Scale Nonlinear Programming." SIAM
Journal on Optimization, Vol 9, No. 4, 1999, pp. 877–900.
[3] Coleman, T. F. and Y. Li. "An Interior,
Trust Region Approach for Nonlinear  Minimization Subject to Bounds." SIAM
Journal on Optimization, Vol. 6, 1996, pp. 418–445. 
[4] Coleman, T. F. and Y. Li. "On the
Convergence of Reflective Newton  Methods for Large-Scale Nonlinear
Minimization Subject to Bounds."  Mathematical Programming,
Vol. 67, Number 2, 1994, pp. 189–224. 
[5] Gill, P. E., W. Murray, and M. H. Wright. Practical
Optimization, London,  Academic Press, 1981.
[6] Han, S. P. "A Globally Convergent
Method for Nonlinear Programming."  Journal of Optimization
Theory and Applications, Vol. 22, 1977, pp. 297. 
[7] Powell, M. J. D. "A Fast Algorithm
for Nonlinearly Constrained  Optimization Calculations." Numerical
Analysis, ed. G. A. Watson, Lecture  Notes
in Mathematics, Springer-Verlag, Vol. 630, 1978. 
[8] Powell, M. J. D. "The Convergence
of Variable Metric Methods For  Nonlinearly Constrained Optimization
Calculations." Nonlinear Programming  3 (O.
L. Mangasarian, R. R. Meyer, and S. M. Robinson, eds.), Academic Press,
1978. 
[9] Waltz, R. A., J. L. Morales, J. Nocedal,
and D. Orban. "An interior algorithm for nonlinear optimization
that combines  line search  and trust region steps." Mathematical
Programming, Vol 107, No. 3, 2006, pp. 391–408.


See Also
 |  |  |  | 





Introduced before R2006a




Was this topic helpful?






















Optimization Toolbox Documentation





Other Documentation





Support